Laboratory Performance
Whilst laboratory automation will bring several immediate direct cost savings, it also offers the potential for significant indirect cost savings. This can be achieved using the information stored during the data capture and related tasks to monitor the analytical efficiency of the laboratory. Analytical errors can be due to several causes. A variety of checks should be included in any analytical system to firstly detect, but also to help quantify and eliminate these errors.
When selecting the type of analytical control samples and checks that are to be included in routine analytical work, it is important to remember that the objective of laboratory control checks is to maintain consistent analytical results over the long term. This applies within the laboratory, as well as between your laboratory and the results produced by other reputable laboratories.
The concept of statistical control used within CCLAS is to identify and remove errors due to assignable causes that are outside a predictable variation. Control limits are used to mark the points within which an analytical result can be expected to fail. The limits can either be determined by statistical methods or defined independently, usually based on experience.
The following table shows apparent analytical errors and possible methods of detecting these errors.
| Error Source | Method of Determining Error |
|---|---|
|
Sampling |
Duplicate samples are repeat samples taken during the preparation or sampling stage. |
|
Contamination |
Blank samples are samples having a zero concentration of the analyte being determined. They may be a blank material (e.g., quartz sand) or just made up of reagent, that are analysed in the same way as the unknown samples. |
|
Analytical bias (accuracy) |
Standard samples are samples of a known expected value that are included within analytical work and are analysed in the same way as unknown samples. |
|
Repeatability (precision) |
Replicate samples, either repeating a given number of samples within a group or repeating each sample during analysis (i.e., two or more samples are taken at the weighing stage). |
|
Controllable random errors |
By definition, there errors are not easily classified, but will often fall into one of the error types above. In any event, they can usually be overcome by using good methodology and adopting good laboratory practices. |
|
Uncontrollable random errors |
The source of these problems may not be found within the laboratory, but come from some outside cause. The above control samples may not indicate the source of the problem (e.g., a power surge could cause a spurious result in a single sample). |
Control Limits
The CCLAS quality control checks use a set of control limits that are normally defined statistically, to identify out of control samples. These tests are carried out relative to two types of control limits:
- Warning limits—These mark the 95% confidence interval on the mean (or expected value). Only 1 in 40 samples is expected above, and 1 in 40 samples expected to be below there limits and yet still be acceptable.
- Action limits—These mark the limits of acceptable results. Analytical work containing control samples with results outside these limits MUST BE REJECTED. These limits mark the 99.8% confidence in the mean (or expected value). Only 1 in 1000 samples is expected below these limits, or 1 in 1000 above and still be correct.
For example, the control limits on a standard sample can be defined as:
Upper Action Limit = EV + 3.09 x SD
Upper Warning Limit = EV + 1.96 x SD
Lower Warning Limit = EV - 1.96 x SD
Lower Action Limit = EV - 3.09 x SD
where:
- EV is the Expected Value, and
- SD is the Standard Deviation (of the distribution about the Expected Value).
The values 1.96 and 3.09 being taken from a statistical table of the area below a normal Gaussian distribution curve and correspond to the nominated confidence intervals above.
Note: The above definitions of control limits assume that the errors of analytical determinations are a normal distribution. In the majority of cases this assumption is acceptable. Some analytical methods are subject to the occasional wild value ( Outliers or Fliers) while other methods may suffer from skewed distributions (for example, at low concentrations negative values may be suppressed by the instrument or operator and not reported; yet some small negative values may be expected because of the normal distribution of errors).
The importance of using unrounded values within the quality control checks is often overlooked. At low concentration in particular, rounding will introduce a stepping effect in the distribution of error that has a large effect on the computed statistics (i.e. rounding to the nearest 1 ppm between 1 and 10 ppm, introduces a stepping error due to rounding alone of up to 10%).
Care should be taken when calculating and using Control Limits in cases where statistical Outliers or Skewed Distribution of errors are suspected.
The Relative Standard Deviation (RSD) is used frequently within CCLAS displays and calculations. It is sometimes referred to as the COEFFICIENT OF VARIATION in older statistical literature and is expressed as a percentage, as:
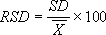
where:
-
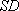is the Standard Deviation (of the distribution about the Expected Value), and -
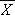is the mean.
Note: The 95% Confidence interval of accuracy approximates to the mean (or expected value) ± two RSD. The 95% confidence interval on precision approximates to twice the RSD. Thus RSD is a very useful measurement of describing and comparing analytical accuracy and precision.
