|
Process Help |
|
Process Name |
Menu Path |
Link to Command Table |
|
VGRAM |
Estimate ribbon | Variograms | Calculate |
Introduction
This process calculates variograms and/or cross variograms for a range of azimuth and dip directions.
How to use
The main benefits are:
-
variograms and/or cross variograms for up to 30 different variables, or one variable with 30 indicator values can be calculated in a single run.
-
automatic calculation of indicator values based on cut-offs.
-
key field options (two key fields are supported, (although three are technically achievable if *BHID is set and &DOWNHOLE = 0) allows variogram calculation to be restricted by the specified key fields e.g. rock type, or BHID to give downhole variograms.
-
key fields options also allows calculation of variograms excluding pairs with the same keyfield value.
-
optimization of sample search for fast calculation.
-
calculations includes normal, relative and lognormal variograms, and covariance.
-
variograms for different directions and the 'directionless' variogram are all calculated in a single run.
-
optional rotated coordinate system ensures flexibility in definition of directions.
-
smaller lag interval for smaller distances.
-
options include angles of regularization, cylindrical radius, lag tolerance, etc.
-
variograms are written to a database file, and/or the print file together with summary statistics.
Rotated Coordinate System
The usual way of defining a set of variogram directions is to define a base azimuth and dip and a set of incremental azimuth and dip angles. Variograms are then calculated for each combination of azimuth and dip. The azimuth is measured clockwise from North (the Y axis), and the dip is measured downwards from the horizontal plane. For example if the base azimuth and dip are both 0o and the horizontal increment is 45o and the vertical increment is 30o then variograms are calculated for azimuth/dip pairs of 0o/ 0o , 0o/ 30o , 0o/ 60o , 0o/ 90o , 45o/ 0o , 45o/ 30o , ..... 315o/ 90o.
Although this method gives variograms for a range of directions it does not allow variograms to be calculated at regular angles in a dipping and/or plunging plane. For example if the main structure of the orebody dips at 25o in the direction N35oE then it would be useful to calculate variograms in this dipping plane. This can be done using parameters AXISn, ANGLEn (n=1,3) to define a set of rotations of the coordinate system. Azimuths and dips are then defined relative to the rotated Y axis which lies in the rotated XY plane.
The ANGLEn and AXISn parameters are defined as follows. The first rotation is by angle ANGLE1 around AXIS1, where AXIS1=1 for the X axis, 2 for the Y axis and 3 for the Z axis. The second and third rotations are defined in an identical manner.
The rotation angle is measured in a clockwise direction when viewed from the positive axis towards the origin. A negative rotation angle means an anticlockwise rotation.
The Y axis after rotation defines the base direction for variogram calculation. Variograms for other directions are all calculated as increments from this base. The azimuth and dip angles of each variogram are written to the results file in both the original (i.e. world) and rotated coordinate systems.
Variogram Directions
Variograms are calculated for a range of directions as defined by six parameters. The initial direction is defined by @AZI and @DIP, which are the azimuth and dip measured relative to the rotated Y axis in the rotated plane. The increments (in degrees) between successive directions are defined by @HORINC and @VERINC, and the number of increments by @NUMHOR and @NUMVER. A variogram is calculated for each combination of azimuth and dip.
A variogram with an azimuth of Ao and a dip of 0o is the same as one with an azimuth of (A+180)o and a dip of 0o. Therefore only the variogram with an azimuth in the range 0o to 180o will be output. Also a variogram with an azimuth of Ao and a dip of Do is the same as an azimuth of (A+180)o and a dip of -Do.
If the range of dip angles includes 90o (vertically downwards from the rotated plane) then this represents a special case which is independent of the azimuth. For this 90o dip case there is a single angle of regularization which is the average of the horizontal and vertical angles @HORANG and @VERANG respectively. This average angle is used to define a cone with a circular cross section. The azimuth for the 90o dip case is recorded in the output file as 0o.
As well as variograms for individual directions, a 'directionless' variogram is also calculated. This is independent of azimuth and dip, and depends only on distance. This is recorded in the output file with azimuth and dip fields both set to absent data (-).
Keyfields
Single keyfield
If a *KEY field is specified then variograms are calculated for each KEY field value. The average variogram over all KEY field values is also calculated. It is NOT necessary for the input sample data file to be sorted on the KEY field.
Parameter @ALLKEYS controls whether the individual variograms are written or whether just the average is written:
|
=0 |
only the average over all KEY field values is written to the output file. This is the default. |
|
=1 |
variograms for all KEY field values and the average variogram are written to the output file. In this case the output file will include the KEY field. If the KEY field is alpha, then the KEY value in the output file for the average variogram is blank; if numeric then it is -. |
Parameter @KEYMETH is also associated with the use of a KEY field:
|
=1 |
calculate variograms within each KEY field, as described above. This is the default. |
|
=2 |
in the variogram calculation only use pairs of samples with different KEY values. If for example the KEY field is BHID, then only pairs of samples in different holes are included. The KEY value written to the output file is blank (alpha) or - (numeric). |
|
=3 |
calculate both the within KEY and different KEY variograms. |
The *KEY field is useful for calculating variograms within the same borehole. It can also be used for calculating variograms within the same rock type.
Where *KEY is specified and @KEYMETH = 2, the output &PAIRSOUT file will contain an attribute for each value of the key field using the format [KEY field Value]n, where n is a unique index. For example, if a keyfield "T" is specified, containing two distinct values throughout the recordset, two attributes will be added to &PAIRSOUT, that is "T1" and "T2". In this case, T1 and T2 would contain different values to reflect the key values for each sample in a pair.
If @KEYMETH were set to 1, the attribute values would still be generated in &PAIRSOUT, but would contain identical values.
The @DOWNHOLE parameter is used to determine if downhole variograms are calculated. You can either set this to either:
-
0 (zero) meaning the BHID field will be treated as an additional KEY field value (effectively, treating the run as having two keyfields, even though only *KEY is specified)
-
1, meaning the BHID field will be used to append any variograms created in the same drillholes. As such, the output file will not include a BHID field. This is the default setting.
@DOWNHOLE is only effective if *BHID is specified.
Two keyfields
VGRAM supports up to two key fields for a single run. For example, you can create both an average variogram and a downhole, directionless variogram using both key fields.
This is achieved using the field specifications *KEY2 and *BHID.
Essentially, if both *KEY and *KEY2 are specified (*KEY2 cannot be set in isolation), both will be affected by the @ALLKEYS and @KEYMETH parameters, for the unique combinations of both specified keys.
As with the single key field scenario, the @DOWNHOLE parameter is used to determine whether downhole parameters are calculated. In a situation where both *KEY and *KEY2 are defined and @DOWNHOLE is set to 0 (zero), this effectively treats the run as having three distinct key fields. However, in this case, if @DOWNHOLE = 1, @ALLKEYS and @KEYMETH will only work for *KEY and *KEY2.
Further notes on dual key field usage in VGRAM:
-
If *BHID is not set, @DOWNHOLE will be ignored (this is the same for single key field usage).
-
If *BHID is specified, downhole variograms will be created in addition to direction and other variograms (as determined by other parameters).
-
If @DOWNHOLE = 0 and *BHID is specified, the behaviour of @ALLKEYS and @KEYMETH will be applied to *BHID (as well as *KEY1 and *KEY2). The downhole variograms will be appended to the file.
-
If @DOWNHOLE = 1 and *BHID is specified, an average downhole variogram (only) will be appended to the file, using the fields *KEY = BHID (and assuming @ALLKEYS = 0 and @KEYMETH = 1). The average downhole variogram will be created for all unique combinations of *KEY and *KEY2. The values of @ALLKEYS and @KEYMETH will apply to *KEY and *KEY2 only.
Lag Interval
There are 3 parameters associated with the definition of the lag:
|
@LAG |
Distance for one lag. |
|
@LAGTOL* |
Tolerance to be used when selecting sample pairs. This is specified in user data units and must be between 0 and half of LAG. If it is not specified or zero then half of LAG is used (-). |
|
@NLAGS* |
Number of lags. The maximum number allowed is 100. |
In addition the initial lags can be divided into sublags. This allows closer
definition of the variogram over smaller distances.
|
@NSUBLAG* |
The number of sublags per lag ie the sublag distance is @LAG/@NSUBLAG. Only the first @NLAGS1 lags are divided. |
|
@NLAGS1* |
The number of lags to be divided into sublags. |
If either @NSUBLAG or @NLAGS1 are - or 0, then sublags are not used.
The maximum number of lags and sublags is 100. For example if @NLAGS=30, @NSUBLAG=4 and @NLAGS= 10, then the number of lags/sublags used iscalculated as:
Lags not divided
into sublags = 30
- 10 = 20
10 lags each divided into
4 sublags = 10 * 4 =
40
Lag 0 divided into 2 sublags = 2
Total =
62
An example of sublags is given here using:
@LAG=10, @NSUBLAG=3, @NLAGS1=2, @LAGTOL= 0
|
Lag |
Lag |
Distance |
Sublag |
Sublag |
Distance |
|
Number |
From |
To |
Number |
From |
To |
|
0 |
0 |
5 |
0 |
0 |
1.667 |
|
0.333 |
1.667 |
5 |
|||
|
1 |
5 |
15 |
0.667 |
5 |
8.333 |
|
1 |
8.333 |
11.667 |
|||
|
1.333 |
11.667 |
15 |
|||
|
2 |
15 |
25 |
1.667 |
15 |
18.333 |
|
2 |
18.333 |
21.667 |
|||
| 2.333 | 21.677 | 25 | |||
| 3 | 25 | 35 | 3 | 25 | 35 |
| 4 | 35 | 45 | 4 | 35 | 45 |
| 5 | 45 | 55 | 5 | 45 | 55 |
The sublag number is written to field LAG in the output variogram file. Note that both the lag and sublag number multiplied by @LAG give the average distance within the lag or sublag except for lag or sublag 0.
Cylindrical Search Constraint
As well as vertical and horizontal angles of regularization the user may define a cylindrical search volume. The cylinder is centered on the variogram direction vector with a user defined radius @CYLRAD. This constraint is in addition to the angles of regularization so that at the smallest lags the pyramid search volume will apply, whereas at larger lags the cylindrical constraint will apply. This is illustrated in Figure 1, below:
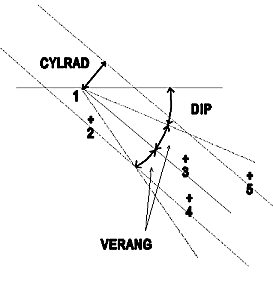
VERTICAL SECTION
Sample 1 is paired with samples 2, 3, 4 and 5 as follows:
SAMPLES PAIR | VERANG Constraint | CYLRAD Constraint | Accept/Reject |
1 and 2 | Fail | Pass | Reject |
1 and 3 | Pass | Pass | Accept |
1 and 4 | Pass | Pass | Accept |
1 and 5 | Pass | Fail | Reject |
similar tests are carried out on possible sample pairs, both in section (as shown above), and in plan (using AZI and HORANG instead of DIP and VERANG). The default value of the optional @CYLRAD parameter is zero, which means that the cylindrical constraint is not applied.
Grade Fields
The grade fields are defined using fields *F1, *F2, ... ,*F24. Only *F1 is compulsory. Up to 24 fields can be defined.
Cross Variogram
Parameter @CROSSVAR is used to control whether variograms and/or cross variograms are to be calculated:
=0 only variograms.
=1 only cross variograms. All possible combinations of *Fi with *Fj (i>j) are calculated.
=2 both variograms and cross variograms are calculated.
If @CROSSVAR = 1 or 2 cross * values will be calculated for the variogram, pairwise relative variogram and log variogram. They will not be calculated for covariance, correlogram or madogram.
Layered Variograms
If the deposit is stratified, it is sometimes useful to calculate variograms within each layer, and also the average over all layers. The base layer plane is defined by the XY plane after the rotations ANGLEn, AXISn have been applied. Layers are defined by 2 parameters:
@SPACING | The samples are assigned a layer number relative to the rotated XY plane. Layer 1 includes all samples between the rotated XY plane and a parallel plane whose rotated Z value is @SPACING. Layer 2 includes all samples between the plane at Z=@SPACING and Z=2*@SPACING. The sample with the minimum Z value (measured in the rotated plane) lies on the plane which is at the base of layer 1. |
@LAYMETH | The layer method: |
| =0 Layers are not used. This is the default. |
| =1 Layers are used, but only the average over all layers is written to the output file. |
| =2 Layers are used, and the variogram for each layer and the average over all layers are written to the output file. Field LAYER is included in the output file. It is set to - for the average over all layers. |
Layers and key fields cannot be used at the same time. If @LAYMETH>=1 and *KEY has been specified then the process terminates with an error message.
If layers are used then variograms will only be calculated for a dip of 0 . Therefore parameters 0o @DIP, @VERINC and @NUMVER which define the initial dip, the incremental angle between dips and the number of increments for the vertical plane will be ignored. The vertical angle of regularization, @VERANG, will still apply.
Indicator Variograms
The process will calculate indicator variograms for a single grade field (*F1) for a range of cutoff values. An indicator takes the value 0 if the grade is less than or equal to cutoff and 1 if it greater than cutoff. If the cutoff values are at regular intervals then the values can be defined by three parameters. If the cutoff values are at irregular intervals, then the cutoffs are defined in file &CUTOFF. If both parameters and file are specified then the &CUTOFF file takes priority. The three parameters are:
@INDSTEP | The step size between successive indicator cutoffs: |
| =0 Do not use indicators, unless a &CUTOFF file has been specified. This is the default. |
| >0 The step size between indicators. |
@INDMIN | The lowest indicator cutoff value. |
@INDNUM | The number of indicators to use; ie indicator variograms will be calculated for cutoffs of @INDMIN, @INDMIN+ 1*@INDSTEP, @INDMIN+ 2*@INDSTEP, ....., @INDMIN+ (@INDNUM - 1)*@INDSTEP. A maximum of 24 cutoffs is allowed. If @INDNUM is greater than or equal to 1 then indicators will be used. |
There are in fact two indicator methods. The first method has been described above and the second method is the Nested Indicator method. In the Nested method a sample is discarded once it has been used. Within the Nested method there are two versions - Bottom-Up and Top-Down. The definition of all three types is shown below.
Ci | is cut-off number i, where 1 ≤ i ≤ n. |
C0 | is set to a very large negative number. |
Cn+1 | is set to a very large positive number. |
n | is the number of cut-offs (n<=24). |
Iil | is the indicator value for cut-off i. |
g | is the grade of a sample. |
Normal Indicator Method:
If g ≤ Ci then Ii = 0
If g >Ci then Ii = 1
Nested Method, Bottom Up:
If g ≤ Ci-1 then Ii = - (absent data)
If Ci-1 < g ≤ Ci then Ii = 0
If g >Ci then Ii = 1
Nested Method, Top Down:
If g ≤ Ci then Ii = 0
If Ci < g ≤ Ci+1 then Ii = 1
If g > Ci+1 then Ii = - (absent data)
These are illustrated in the following example:
Sample Grade | Cut-Off | Normal | Method | Cut-Off Bottom Up . | Cut-Off Top Down | ||||
1.5 | 2.5 | 3.5 | 1.5 | 2.5 | 3.5 | 3.5 | 2.5 | 1.5 | |
7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | - | - |
2.3 | 1 | 0 | 0 | 1 | 0 | - 0 | 0 | 1 |
|
0.5 | 0 | 0 | 0 | 0 | - | - | 0 | 0 | 0 |
2.7 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | - |
4.2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | - | - |
An indicator value of - means that the sample is not u sed in the variogram calculation for that cutoff.
The indicator method is controlled by parameter:
@NESTED | =0 | The Normal Indicator method is used. This is the default. |
| =1 | Nested Method, Bottom Up. |
| =2 | Nested Method, Top Down. |
If indicators are selected then only variograms, not cross variograms, are calculated.
The Variogram Output File
The variogram output file includes the fields shown below. Fields without a * are always created. Fields followed by a * are only created under certain conditions as described.
GRADE | The grade field for variograms, or the first grade field for cross variograms. |
GRADE2* | The second grade field. This is only created if cross variograms are calculated. If both variograms and cross variograms are output, then for variograms the GRADE and GRADE2 fields will be the same. |
CUTOFF* | Cutoff grade for indicator variograms. This is only created if indicator variograms are calculated. |
[KEY]* | The key field value, alpha or numeric. This is only included if *KEY has been specified, and @KEYMETH & 2. The [] brackets mean that the field name in the file is not KEY, but whatever field has been selected as the KEY field. |
KEYMETH* | A numeric flag field which is only created if *KEY has been specified and @KEYMETH = 3; ie both the same key and different key variograms are calculated. It is set to 1 for the same key variograms, and to 2 for the different key variograms. Notes about @KEYMETH and &PAIRSOUT
|
LAYER* | The layer number. This is only included if @LAYMETH = 2 ie variograms are output for individual layers. The sample with the minimum Z value (measured in the rotated plane) lies on the plane which is at the base of layer 1. AZI The azimuth of the variogram measured clockwise from the Y axis in the rotated plane. DIP The dip of the variogram measured downwards from the rotated XY plane. |
WAZI* | The azimuth of the variogram, in the world coordinate system. This is only included if one or more rotation angles (@ANGLEn) have been defined. If rotation angles are not defined, then WAZI and AZI would have the same value. |
WDIP* | The dip of the variogram, in the world coordinate system. This is only included if one or more rotation angles (@ANGLEn) have been defined. If rotation angles are not defined, then WDIP and DIP would have the same value. |
LAG | The lag, or sublag number. |
AVE.DIST | The average distance between samples for the current lag. |
NO.PAIRS | The number of pairs of samples for the current lag. |
COVAR | The covariance between sample pairs. For a variogram this is calculated as:
COVAR = ( ∑ xi xi+h - ∑ xi ∑ xi+h / n ) / (n - 1)
For a cross variogram COVAR is calculated as: |
| COVAR = ( ∑ (xi yi+h + xi+h yi)- (∑ (xi +xi+h ) ∑ (yi + yi+h ) / 2n )) / (2n - 1) |
VGRAM | The variogram or cross variogram value. The variogram is defined as: |
| g(h) = ∑ (xi - xi+h )2 / 2n |
| and the cross variogram is defined as: |
| g(h) = ∑ [(xi - xi+h ) (yi - yi+h )] / 2n |
| where xi is the value of one grade (eg AU) at location i, and yi is the value of the second grade field (eg AG) at location i. |
PWRVGRAM | The pairwise relative variogram or relative cross variogram. This is the same as the variogram or cross variogram, except that every term in the calculation is divided by the average value of the two samples contributing to that term. The pairwise relative variogram is calculated as: |
| g(h) =∑ [ (xi - xi+h )2 / (0.5 (xi + xi+h ) )2 ] / 2n |
| The pairwise relative cross variogram is calculated as: |
| g(h) = ∑ [(xi - xi+h ) (yi - yi+h ) / (( 0.5 (xi + xi+h)) ( 0.5 (yi + yi+h ))) ] / 2n |
LOGVGRAM | The log variogram or cross variogram. This is calculated by taking the logs of the grade values before calculating the variogram or cross variogram. If a grade is less than @LOGCON then its value is replaced by @LOGCON. |
MADOGRAM | this is similar to
the variogram; instead of squaring the difference between xi and xi+h the
absolute difference is used: g(h) = ∑ abs(xi - xi+h ) / 2n |
CRLOGRAM | the correlogram is the correlation coefficient calculated between pairs of samples a distance h apart |
NSAMPLE | The number of individual samples contributing to the variogram or cross variogram. This field remains constant for each variogram or cross variogram, and the same applies to the following 6 fields. |
AVGRADE | The average (ie mean) grade or average indicator value over all samples used for calculating the current variogram or cross variogram for field GRADE. |
AVGRADE2* | The average (ie mean) grade or average indicator value over all samples used for calculating the current cross variogram for field GRADE2. |
VRGRADE | The variance of the grade or indicator, over all samples used for calculating the current variogram. In the case of cross variograms VRGRADE is the covariance between the two variables. |
AVLGRADE* | The average (ie mean) grade of the logs over all samples used for calculating the current variogram or cross variogram for field GRADE. This field is not created if indicators are used. |
AVLGRAD2* | The average (ie mean) grade of the logs over all samples used for calculating the current cross variogram for field GRADE2. This field is not created if indicators are used. |
VRLGRADE* | The variance of the log of the grade, over all samples used for calculating the current variogram. In the case of cross variograms VRLGRADE is the covariance between the logs of the two variables. This field is not created if indicators are used. |
ANGLE1* | Rotation angle 1. Only included if one or more of the rotation angles are nonzero. This is an implicit field. |
AXIS1* | Rotation axis 1. Only included if one or more of the rotation angles are nonzero. This is an implicit field. |
ANGLE2* | Rotation angle 2. Only included if one or more of the rotation angles are nonzero. This is an implicit field. |
AXIS2* | Rotation axis 2. Only included if one or more of the rotation angles are nonzero. This is an implicit field. |
ANGLE3* | Rotation angle 3. Only included if one or more of the rotation angles are nonzero. This is an implicit field. |
AXIS3* | Rotation axis 3. Only included if one or more of the rotation angles are nonzero. This is an implicit field. |
The Sample Pairs Output File
The sample pairs output file contains one record for each sample pair used to calculate a variogram or cross variogram. If specified it will be created with the following fields:
VLAGDIST | Variogram lag value. |
VDIP,VAZI | The dip and azimuth direction 'bin' for the current pair of samples in the rotated coordinate system. If a pair contributes to more than one variogram 'bin' then a record is output for each bin. The two angles are measured in the rotated coordinate system. |
WVDIP,WVAZI* | The same as VDIP and VAZI except in the world coordinate system. If all rotation angles are zero, then the values are the same as VDIP and VAZI and so the two fields WVDIP and WVAZI are not output. |
DISTANCE | Actual distance between samples. |
DIP,AZI | Actual angles between samples in the rotated coordinate system. |
WDIP, WAZI* | These are the same as DIP and AZI, except that they are measured in the world coordinate system. If all rotation angles are zero, then the values are the same as DIP and AZI and so the two fields WDIP and WAZI are not output. |
X1,Y1,Z1* | Coordinates of 1st sample point. If Z is not specified then only X and Y are included. |
X2,Y2,Z2* | Coordinates of 2nd sample point. If Z is not specified then only X and Y are included. |
GRADE1 | Grade field for variogram or first grade field for cross variogram. |
GRADE2* | Second grade field for cross variogram. Not used for a variogram. |
VALUE11 | Value of the 1st sample GRADE1. |
VALUE12 | Value of the 2nd sample GRADE1. |
VALUE21 | Value of the 1st sample GRADE2. |
VALUE22 | Value of the 2nd sample GRADE2. |
Note that care should be taken when specifying this output file as its size may be depending on the number of samples, variograms and lags.
Displayed Output
The @PRINT parameter controls the amount of information sent to t he display. If it is set to 0 then there is just a summary of the input data. The variograms are written to the output file but are not displayed on the screen or sent to the print file.
If @PRINT=1 (the default) then each variogram will be displayed on the screen. The number of lines per screen is controlled by the @PROMPT parameter. If @ECHO=1 then the same information is also sent to the print file. However the value of @PROMPT is not used for paging the print file. Each variogram is started on a new page.
The display of variogram tables on the screen can be terminated at any stage using '!'. This does not affect the variogram tables sent to the print file. A progress monitor shows the percentage of the total variogram calculations which have been completed. It also shows the estimated time to completion and the estimated completion time.
Run Times
The main factor contributing to the run time of process VGRAM is the number of samples in the input sample data file. If the process has to pair eve ry sample with every other sample then there is a limited amount that can be done to reduce the run time. In this case the run time is approximately proportional to the number of samples. However if the maximum lag distance (@NLAGS*@LAG) is significantly less than the maximum separation between samples then the sample search optimizing method can reduce the run time substantially.
The optimizing method divides the area covered by the samples into a three dimensional grid and the samples are indexed accordingly. Sample pairs are only considered if they lie within blocks which are separated by less than the maximum lag distance. Therefore it is best to select the @LAG and @NLAG parameters so that the total distance is sufficient to cover the range of interest, but is not unnecessarily large.
Compatibility With GSLIB
For some variogram programs, such as in GSLIB, the angles of regularization are measured in the horizontal and vertical directions respectively. This means that for the steeper dips the actual volume within the angles of regularization reduces as the dip increases. This is illustrated in the diagram which shows the intersection of the volume of regularization with the surface of a sphere.
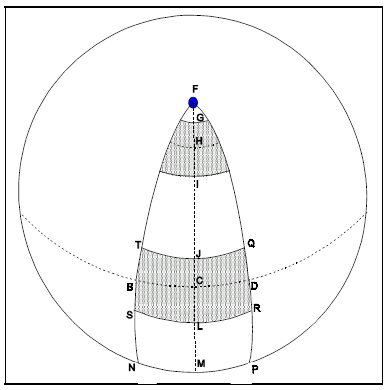
Points B, C, and D all have zero dip, and so the broken line BCD lies on the equator. The broken line FM is a line of longitude (azimuth a), with point F being the North Pole. If point O (not shown in the diagram) is at the centre of the sphere then line OC is the vector of a variogram with zero dip and azimuth a. The lines of longitude FTBSN and FQDRP are the limits of the horizontal angle of regularization around OC. The lines of latitude TJQ and SLR are the upper and lower limits of the vertical angle of regularization.
The lower shaded area represents the intersection of the volume of regularization with the surface of the sphere. This volume is associated with vector OC, which has azmiuth " and zero dip. The upper shaded area represents a similar intersection, but for vector OH which also has azimuth ", but a large negative dip (about -75 in the diagram). It can be seen that the surface area of of intersection and hence the volume of regularization decreases as the dip gets further from zero (in either the positive or negative directions).
VGRAM has been designed so that the volume of regularization is constant, and is independent of the dip. This is done by transforming the data so that th e vector has a dip of zero in the rotated system. Hence the intersection of all volumes of regularization are equivalent to the lower shaded area. This means that there will be an overlap between volumes of regularization. Some sample pairs will be used for more than one variogram. The end result is that if there is a regular distribution of samples then using VGRAM the number of sample pairs for lag N will be the same whatever the azimuth and dip of the variogram. This is not the case for GSLIB where the volume of regularization and hence the number of sample pairs decreases as the dip gets further from zero.
Files, Fields and Parameters
Input Files
Name | Description | I/O Status | Required | Type |
IN | Input sample data file. This must contain the fields X and Y , and at least one grade field F1. The Z field is optional. This file must also contain the KEY field, if it has been specified. | Input | Yes | Undefined |
CUTOFF | This contains the cut-off grades for indicator variograms. There is a single field CUTOFF, and up to 24 records, one per cut-off. The file does not have to be sorted on CUTOFF. | Input | No | Variogram - Model |
Output Files
Name | I/O Status | Required | Type | Description |
OUT | Output | Yes | Undefined | Variogram output file. This will contain the fields described previously. The name must not be the same as the input file. |
PAIRSOUT | Output Notes about @KEYMETH and &PAIRSOUT
| No | Undefined | The sample pairs output file containing one record for each sample pair used to calculate a variogram or cross variogram. |
Fields
Name | Description | Source | Required | Type | Default |
X | X coordinate of sample data. The default field name is X. | IN | No | Numeric | X |
Y | Y coordinate of sample data. The default field name is Y. | IN | No | Numeric | Y |
Z | Z coordinate of sample data. This field is optional, but if field Z exists in the sample data file it will be used. | IN | No | Numeric | Z |
F1-30 | Grade fields for variogram and/or cross variogram. At least one field must be specified. Up to 29 additional fields can be specified. | IN | Yes for F1, No for second and subsequent fields. | Numeric | Undefined |
KEY1-5 | Key field. Variograms are calculated for each key field value. Notes about @KEYMETH and &PAIRSOUT
| IN | No | Any | Undefined |
BHID | Borehole identification field. Used with:
| IN | No | Any | Undefined |
Parameters
Name | Description | Required | Default | Range | Values | ||||||||
LAG | Distance for one lag. | Yes | Undefined | Undefined | Undefined | ||||||||
LAGTOL | Tolerance to be used when selecting sample pairs. This is specified in user data units and should be between 0 and half of LAG. If not specified or not within this range then half of LAG is used (-). If sublags are used, then the tolerance for a sublag is LAGTOL/ NSUBLAG. | No | - | Undefined | Undefined | ||||||||
NLAGS | Number of lags. The maximum is 9999. The default is (25). | No | 25 | 1,9999 | Undefined | ||||||||
NSUBLAG | The number of sublags per lag ie the sublag distance is LAG/ NSUBLAG. Only the first NLAGS1 lags are divided. (0). | No | 0 | Undefined | Undefined | ||||||||
NLAGS1 | The number of lags to be divided into sublags. (0). | No | 0 | Undefined | Undefined | ||||||||
AZI | Azimuth of first variogram, measured in degrees from the Y axis in the rotated plane. 0 degrees is in the direction of the positive Y axis. 90 degrees is in the direction of the positive X axis. Default (0). | No | 0 | 0,360 | Undefined | ||||||||
HORANG | Azimuth regularisation angle, measured in degrees. The angle range taken is AZI + or - HORANG. Default (90). | No | 90 | Undefined | Undefined | ||||||||
HORINC | Azimuth increment angle in degrees measured in the rotated plane. Variograms are calculated for azimuths AZI , AZI + HORINC , AZI + 2 AZI + [ NUMHOR-1] | No | 0 | Undefined | Undefined | ||||||||
NUMHOR | Number of azimuths. The maximum number of individual variograms calculated is NUMHOR | No | 1 | Undefined | Undefined | ||||||||
DIP | Dip direction of first variogram, measured in degrees in direction of the negative Z axis in the rotated plane. A dip angle of 0 is in the rotated X-Y plane [usually horizontal], a dip of 90 is in the negative Z direction [vertically downwards] and a dip of -90 is in the positive Z direction [vertically upwards] (0). | No | 0 | -90,90 | Undefined | ||||||||
VERANG | Dip regularisation angle, measured in degrees. The angle range is taken as DIP + or - VERANG. The default is (90). | No | 90 | -90,90 | Undefined | ||||||||
VERINC | Dip increment angle in degrees measured in the rotated plane. Variograms are calculated for dips DIP , DIP + VERINC , DIP + 2 ......, DIP + [ NUMVER-1] | No | 0 | Undefined | Undefined | ||||||||
NUMVER | Number of dips. The maximum number of individual variograms calculated is NUMHOR | No | 1 | Undefined | Undefined | ||||||||
CYLRAD | Cylindrical search radius (0). Zero means cylindrical search constraint not applied. | No | 0 | Undefined | Undefined | ||||||||
ALLKEYS | This parameter controls whether the individual variograms are written or whether just the average is written. (0).
| No | 0 | 0,1 | 0,1 | ||||||||
KEYMETH | Controls how keys are applied. (1).
Notes about @KEYMETH and &PAIRSOUT
|
No | 1 | 1,3 | 1,2,3 | ||||||||
DOWNHOLE | Controls whether the downhole variograms are calculated.
| No | 1 | 0,1 | 0,1 | ||||||||
KEYTOL | The tolerance used to test whether numeric keyfields are equal. This should be set to greater than or equal to zero. If a negative value is specified then zero is used. If explicitly set to absent (in a macro) then zero is used. | No | 0.00001 | Undefined | Undefined | ||||||||
CROSSVAR | Controls whether variograms and/or cross variograms are to be calculated. (0).
| No | 0 | 0,2 | 0,1,2 | ||||||||
INDSTEP | The step size between successive indicator cutoffs. (0). =0 Do not use indicators, unless a CUTOFF file has been specified. This is the default. >0 The step size between indicators. | No | 0 | Undefined | Undefined | ||||||||
INDMIN | The lowest indicator cutoff value. (0). | No | 0 | Undefined | Undefined | ||||||||
INDNUM | The number of indicators to use; ie indicator variograms will be calculated for cutoffs of INDMIN , INDMIN+ 1 INDSTEP , INDMIN+ 2 INDSTEP , ..... , INDMIN+ [ INDNUM - 1]* INDSTEP. A maximum of 24 cutoffs is allowed. (0). | No | 0 | Undefined | Undefined | ||||||||
NESTED | Method for calculating indicators. (0).
| No | 0 | 0,2 | 0,1,2 | ||||||||
ANGLE1 | First rotation angle, in degrees. (0). | No | 0 | Undefined | Undefined | ||||||||
AXIS1 | First rotation axis. 1=X, 2=Y, 3=Z. The first rotation is by ANGLE1 degrees clockwise around axis AXIS1 , when viewed along the axis from positive values towards the origin. An axis value of 0 means no rotation. (3). | No | 3 | 1,3 | 1,2,3 | ||||||||
ANGLE2 | Second rotation angle, in degrees. (0). | No | 0 | Undefined | Undefined | ||||||||
AXIS2 | Second rotation axis. 1=X, 2=Y, 3=Z. The second rotation is by ANGLE2 degrees clockwise around axis AXIS2 , when viewed along the axis from positive values towards the origin. An axis value of 0 means no rotation. (1). | No | 1 | 1,3 | 1,2,3 | ||||||||
ANGLE3 | Third rotation angle, in degrees. (0). | No | 0 | Undefined | Undefined | ||||||||
AXIS3 | Third rotation axis. 1=X, 2=Y, 3=Z. The first rotation is by ANGLE3 degrees clockwise around axis AXIS3 , when viewed along the axis from positive values towards the origin. An axis value of 0 means no rotation. (3). | No | 3 | 1,3 | 1,2,3 | ||||||||
LOGCON | If the sample value is less than LOGCON , then it is substituted by the value of LOGCON in the calculation of the logarithmic variogram (0.001). | No | 0.001 | Undefined | Undefined | ||||||||
ADDCON | Constant added to VALUE field before calculation of log variograms or log statistics (0). | No | 0 | Undefined | Undefined | ||||||||
LAYMETH | The layer method. If the deposit is stratified it is often useful to calculate variograms with in each layer, and also the average over all layers. The base layer plane is defined by the XY plane after the rotations ANGLEn, AXISn have been applied. Layers are defined by 2 parameters. (0). =0 Layers are not used. This is the default. =1 Layers are used, but only the average over all layers is written to the output file. =2 Layers are used, and the variogram for each layer and the average over all layers are written to the output file. Field LAYER is included in the output file. It is set to - for the average over all layers. | No | 0 | 0,2 | 0,1,2 | ||||||||
SPACING | The samples are assigned a layer number relative to the rotated XY plane. Layer 1 includes all samples between the rotated XY plane and a parallel plane whose rotated Z value is SPACING. Layer 2 includes all samples between the plane at Z= SPACING and Z=2 SPACING. The sample with the minimum Z value [measured in the rotated plane] lies on the plane which is at the base of layer 1. If SPACING = 0 then layers are not used. | No | 100 | Undefined | Undefined |
Notes
A progress report is displayed during execution of the VGRAM process summarizing the percentage of the variogram calculation which has been completed. The progress report also shows the estimated time remaining and the estimated time of completion.
Example
!VGRAM
| &IN(DATA0),&OUT(VGOUT1A),&PAIRSOUT(pairsout), @HORINC=30.0,@NUMVER=4.0,@VERINC=30.0,@ALLKEYS=0.0,@KEYMETH=1.0,@CROSSVAR=0.0, @INDSTEP=0.0,@INDMIN=0.0,@INDNUM=0.0,@NESTED=0.0, @PRINT=1.0,@ECHO=1.0,@ANGLE1=30.0,@AXIS1=3.0,@ANGLE2=25.0, @AXIS2=1.0,@ANGLE3=0.0,@AXIS3=3.0,@LOGCON=0.001, @ADDCON=0.0,@LAYMETH=0.0,@SPACING=20.0,@PROMPT=20.0 |
Variogram Calculation - Input Summary
-------------------------------------
Variogram calculation for 2 field(s) as follows:
AU AG
Variograms will be calculated for each value of key field: ZONE
Only the average variogram(s) over all key field values will be reported.
The reference plane will be rotated as follows:
30.00 degrees around the Z axis.
25.00 degrees around the X axis.
Variograms will be calculated for the directions and dips shown below.
In addition a variogram independent of direction and dip will be calculated.
Initial direction: .00
+ or - 22.50 degrees
Initial dip: .00
+ or - 15.00 degrees
Increment between successive directions: 30.00
degrees
Increment between successive dips: 30.00
degrees
Number of directions: 8
Number of dips: 4
A cylindrical search radius of 12.00 will be used.
Lag intervals are defined as follows:
Number of lags: 10
Lag distance: 5.00
Lag tolerance: 2.50
Sublags per lag: 2
Lags with sublags: 1
>>> 100854 sample pairs, 100.0% completed. Time: 9:54:37 <<<
You may terminate the displayed output at any time by entering ! then
<RETURN>.
This does not affect the contents of the &OUT file which is already
complete.
Neither does it affect the conntents of the print file.
>>> PRESS <RETURN> TO CONTINUE (OR ! TO TERMINATE) >
===============================================================================
Variogram for grade: AU
Average over key field: ZONE
Variogram is independent of direction and dip.
Number of samples: 1000
Mean: 6.132 Variance: 27.489
Log Mean: 1.533 Log Variance: .558
Lag Average Number Covariance Variogram Pairwise Log
Distance of
Pairs Rel.Vgram Variogram
.25 1.43 6 -9.609 34.713 .432 .630
.75 4.14 47 -1.106 26.601 .293 .424
1.25 6.35 153 -.759 25.407 .372 .532
2.00 10.30 760 -.747 23.818 .377 .552
3.00 15.25 1667 2.087 22.926 .363 .528
4.00 20.18 2834 -.348 24.953 .365 .532
5.00 25.17 4156 .345 24.996 .362 .530
6.00 30.09 5532 -.290 27.290 .383 .569
7.00 35.09 6948 -.084 26.258 .373 .554
8.00 40.05 8004 -.027 24.618 .370 .540
9.00 45.06 9178 -.388 26.282 .378 .560
10.00 48.76 4842 -.328 24.667 .381 .562
>>> PRESS <RETURN> TO CONTINUE (OR ! TO TERMINATE) >
===============================================================================
Variogram for grade: AU
Average over key field: ZONE
Local direction: .00
+ or - 22.50 World direction: 30.00
Local dip: .00
+ or - 15.00 World dip: 25.00
Number of samples: 1000
Mean: 6.132 Variance: 27.489
Log Mean: 1.533 Log Variance: .558
Lag Average Number Covariance Variogram Pairwise Log
Distance of
Pairs Rel.Vgram Variogram
.75 4.81 1 .000 68.441 .993 1.536
1.25 6.18 12 -3.676 36.142 .468 .665
2.00 10.44 47 4.937 21.989 .324 .430
3.00 15.16 111 2.947 24.229 .387 .550
4.00 20.27 193 .395 19.282 .335 .475
5.00 25.25 254 .394 25.704 .362 .540
6.00 30.15 323 .818 32.793 .382 .557
7.00 34.89 343 1.019 23.935 .369 .551
8.00 39.91 329 -1.559 35.146 .403 .595
9.00 44.95 334 1.487 27.714 .363 .543
10.00 48.70 160 1.463 30.222 .368 .525
>>> PRESS <RETURN> TO CONTINUE (OR ! TO TERMINATE) >!
>>> 536 RECORDS IN FILE VGOUT1A <<<
>>> 187736 RECORDS IN FILE PAIRSOUT <<<
Error and Warning Messages
A comprehensive check of files, fields and parameters is carried out before the variogram calculation starts. Warning and error messages are displayed as appropriate.

