Underground Alternative Method - Details

In your application, you can choose to automatically assess the different block values arising from both above-ground and underground methods and establish the most appropriate ultimate pit considering an underground mine.

Find out more about how your application can adopt the underground alternative method...

Open Pit Optimization Considering an Underground Alternative

(Original article by Juan P. Camus - full accreditation and source link follows)

One of the most important decisions in mine development is the selection of the mining method.

Open pit or underground methods are selected depending on the shape of the deposit and its position with respect to the surface. Sometimes this decision is not clear or evident. In these cases, the common rule is to compare underground and open pit projects to choose which yields the maximum return. However, in some circumstances, the best alternative is to start the operation with an open pit until a point where mine operating costs make it more convenient (and profitable) to employ an underground method. In this case, the final pit limit is not directly related to commodity prices and its overall shape is a function of capital and operating costs associated with both methods.

Methodology

This approach consists basically in running the open pit algorithm taking into account the alternative cost due to the underground exploitation. For this purpose a three dimensional block model of the deposit is required; then each block of the model should be valued considering the income and relevant costs of both methods.

Let Bop and Bug be the net economic values of a block relating to open pit and underground exploitation respectively.

If the block is going to be extracted by open pit, then it has to pay its stripping cost as well as the potential underground benefit, such as is explained in the following example:

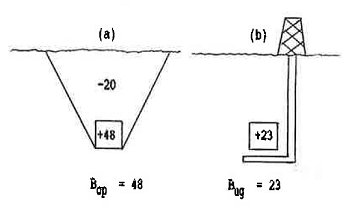
The above image (a) shows a block which can be extracted by open pit and (b) presents the same block, but with the possibility of being extracted by underground works. The net economic value of each block is +48 for open pit and +23 for underground. The stripping cost associated with open pit mining is -20. Capital investment required to build the shaft and other developments are included in the underground benefit (+23).

The figures indicate that open pit mining yields a total benefit of +28 against +23 that is generated by underground mining. To guarantee that open pit is always better than underground, the right block valuation procedure to be used, prior to running the open pit routine, should be:

B = Bop- Bug

In the previous example, B is equal to +25 and this benefit is greater than the stripping cost (-20); so it is better to extract the block by open pit rather than underground. The principle is especially useful when an orebody is represented by a block model and, due to the great number of blocks, the solution is not as obvious as in the preceding exercise.

It is important to note that the open pit cost differs from the underground value principally because of mining costs and dilution factors associated with the last method. Hence, the above expression is, in general, independent of the commodity price and of the costs beyond mining activities such as treatment charges or any other expenditure not concerned with the mine. Furthermore, parameters such as head grade, mill recovery and others do not affect directly the value of B in the equation. For these reasons, the optimal pit obtained with this procedure depends principally on the economic features of mining methods (costs and dilution).

It is convenient to understand that this approach is conceived to find the place or the time at which underground works replace surface operations. As with many optimization techniques, the solution itself does not indicate whether the final pit produced is profitable. To overcome this problem it is advisable to design a traditional pit limit (within underground constraint); thus, if the optimized solution is inside the unrestricted shell, then it is possible to assume that the proper pit limit is profitable. Obviously, if the ore left out of of the right pit limit is insufficient to justify an underground exploitation, the best pit boundary is the one obtained by conventional procedures.

Another point which should be carefully considered in block valuation is the treatment of capital investment expenditures. There is not a general rule to solve this problem, nevertheless, some comments may be useful. Firstly, the unique capital expenditures that would directly affect the proper pit design are those required to operate the mines. Other capital investments, such as plant facilities engineering, exploration etc. only have a repercussion on project profitability rather than on optimal pit outline. Secondly, the relevant mining capital expenditures are those which can be avoided if production stops. THese are commonly investments required for mine equipment replacement in open pit mining and investments for infrastructure and development in underground mining.

To include these expenditures and other fixed overhead costs in block valuation, some assumptions about mining and milling capacities should be considered. If it is expected that processing facilities impose a limit on the rate at which ore can be treated, these costs should be expressed on a per-tonne-of-ore basis. On the other hand, if mine capacity imposes a limit on the rate of progress through the ore body, these costs should be expressed on a per-tonne-of-material (ore plus waste) basis. But, as the total ore and waste tonnage to be exploited either by open pit or underground methods is unknown prior to block valuation, a trial-and-error technique should be followed. This is a chicken and egg problem which is typical in mine planning activities; the final solution has therefore to be iterative, gross initial assumptions being refined later as the shape of the problem becomes clearer.

Underground Alternative Method Case Study

The following explains how the preceding concepts should be applied in a hypothetical case; the exercise is based upon a 2D block model, illustrating 6 blocks with their respective copper grade (% CU):

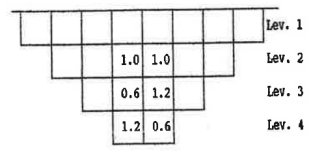
The boundary conditions are the following:

Copper price = US$ 1,800/ton
Copper recovery = 80%
Treatment costs = US$ 500/ton
Other expenditures = US$ 100/ton
Mining costs

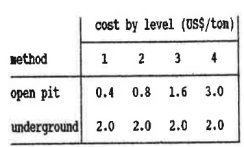
Block weight = 1 ton
Slope angle = 45 degrees
In the case of underground mining, no capital investment and dilution factors have been considered.
In the open pit case, it is supposed that mining is carried out by a contractor and no capital investment is required.

The objective is to the find the best strategy to exploit the deposit.

Solution 1: Open Pit Alternative

This case considers only an open pit exploitation and each block of the inventory is valued according to the following formula:

Where,

Bop = block revenue or cost (US$)
P = copper price (US$/ton)
t = treatment costs (US$/ton)
c = other expenditures (US$/ton)
g = average grade (% Cu)
r = metallurgical recovery (%)
m1 = open pit mining costs (US$/ton)
T = block tonnage

The image below shows the 2D block model and each block appears with its net revenue (US$); superimposed is the final pit limit which yields the maximum benefit (US$ 33.4). The bottom right block is left outside the shell because it does not pay its stripping cost:

Solution 2: Underground Alternative

On the other hand, this case considers only an underground exploitation and each mineralized block is valued as follows:

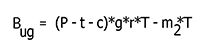
Where,

Bug = block revenue (US$)
m2 = underground mining cost (US$/ton)

The waste blocks are considered with zero value because they were left in situ. The total benefit which is obtained in this case is US$ 41.76 such as illustrated below:

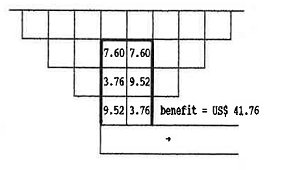
Solution 3: Optimized Alternative

The approach described in this paper should consider an open pit optimization taking into account an alternative cost due to an underground exploitation. The block model is then valued considering the formula:

B = Bop- Bug

The image below shows the block values and the final pit limit obtained when the new optimization procedure is performed:

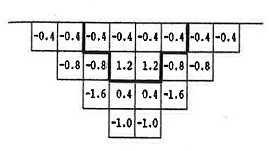
This result entails to exploit the upper part of the ore body by open pit method and the bottom one by underground works. The total benefit associated with this strategy is $US 42.56 which consists of US$16 of open pit plus US$ 26.56 of underground benefit, as shown below:

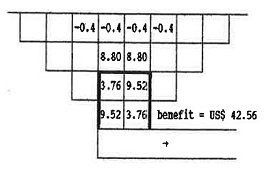
The following table summarizes the results obtained in this hypothetical example:

ALTERNATIVE	ORE (ton)	AV. GRADE (% Cu)	BENEFIT (US$)
Open pit	5	1.00	33.40
Underground	6	0.93	41.76
Combined	6	0.93	42.56

Information presented in this article is from "Open Pit Optimisation Considering an Underground Alternative" by Juan P. Camus, presented as part of the proceedings of the 23rd International Symposium on the Application of Computers and Operations Research in the Mineral Industry (APCOM) held in Tucson, AZ, USA, from April 7 to 11, 1992. Juan's paper is reproduced in part with minor corrections.

Further references:

Lemieux, Marc, 1979 "Moving cone optimizing algorithm" Computer methods for the 80s in the mineral industry, SWE/AIME, New York

Wilsson, Dan, 1982, "Open pit or underground mining", Underground mining methods handbook, SWE/AIME, New York

Article Source:

https://www.worldcat.org/title/23rd-application-of-computers-and-operations-research-in-the-mineral-industry/oclc/26335886

	Related Topics
	Underground Alternative Method Economic Model Essentials Pit Optimization Essentials