Sequential Gaussian Simulations

The Conditional Sequential Gaussian Simulation procedure enables you to perform several simulations of several numerical variables in the multi-gaussian framework using the Sequential Gaussian technique. All simulations replicate the model given in input and are constrained to adhere to all the active information (hence the name of conditional simulation).

Note: Isatis offers two algorithms for sequential gaussian simulations. This one is based on a sequential neighborhood search when the other one is based on a standard Isatis neighborhood with a better theoretical implementation.

This method consists of two steps. Firstly, a random path through all the target points of the simulation domain is defined (unique for all the realizations for a faster implementation). Each target point is then simulated in turn according to a conditional gaussian distribution, taking into account all the values previously generated for all the previous points. In gaussian framework, the simulated value is obtained as follows:

where Z_K is the simple kriging estimate, the attached standard deviation and U a random normal function.

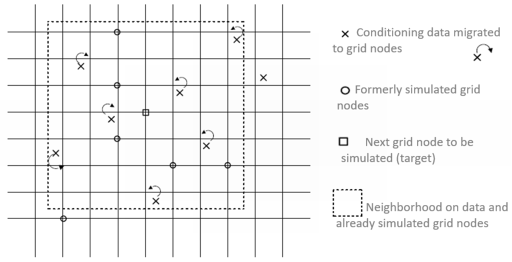
In practice, the simulation domain has often too many target points and the procedure cannot be applied directly. Instead, the simulation of each point requires a selection of the already generated values. A sequential neighborhood is established, centered on the target grid node, whose extension is defined by its radius in grid meshes. Within this neighborhood, the procedure searches for data and for already simulated grid nodes, whose respective maximum counts are specified by the user. The search is performed by decreasing distance through the covariance function which ensures that the data most closely correlated with the target are taken first.

This limitation is the major drawback of the method. As the method is based on simple kriging, a strict stationarity is required.

Note: The algorithm first requires the migration of each input data point to its closest grid node. The exact data locations are not kept. Only the points covered by the target grid (with a tolerance equal to half the size of the grid mesh) are effectively considered in the procedure, the other ones are ignored.

Note: In the multivariate case, at each target node, only one cokriging step is performed and each variable is then simulated. A proper solution is used in the other implementation of SGS which is considered as more CPU time consuming.