Spill Point Calculation

Introduction

In Oil & Gas applications, the spill point calculation enables the user to delineate a potential reservoir knowing that some control points are inside or outside the reservoir.

For the illustration of this feature, we will consider one map (which may be one of the outcomes of a simulation process) where the variable is the topography of the top of a reservoir. We will consider the depth as counted positively downwards: the top of the structure corresponds to the lowest value in the field.

Moreover, we assume that we have a collection of control points whose locations are known and which belong to one of the following two categories:

the control point belongs to the reservoir: inside,
the control point does not belong to the reservoir: outside.

Note: All the points located outside the frame where the image is defined are considered as outside.

Basic Principle

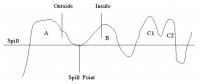
The principle is to find the elevation of the deepest horizontal plane which will split the field into inside and outside sub-areas while remaining compatible with the control point information (the Spill). We also look for the crucial point where, if the Spill is slightly increased, the violation of the constraints will first take place (the Spill Point). The following figure illustrates these definitions:

The Spill Point corresponds to the location of the saddle below volumes A and B. As a matter of fact, if we consider a deeper spill, these two volumes will connect and the constraints induced by the control points will not be fulfilled any more as the same location cannot be simultaneously inside and outside the reservoir.

The volume A is considered as outside whereas B is inside. An interesting feature comes from the volumes C1 and C2:

they are first connected (as elevation of the separation saddle is located above the spill point) and therefore constitute a single volume C,
the contents of this volume C is unknown.

Hence, after the spill point elevation has been calculated, each point in the frame can only correspond to one of the following four status:

below the spill point,
above the spill point and inside the reservoir,
above the spill point and outside the reservoir,
above the spill point in an unknown volume.

Maximum Reservoir Thickness Constraint

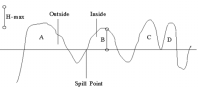
This constraint corresponds to an actual limitation that must be taken into account in the Oil Industry. Due to the quality of the rock and the depth of the reservoir, the pressure of the captured fluid implies the thickness of the reservoir not to exceed a maximum value. This constraint is referred to as the maximum reservoir thickness. On the previous figure, let us add this constraint:

The new spill point is shifted upwards as otherwise the maximum reservoir thickness constraint would be violated. Note that, the Spill elevation is clearly known whereas the location of the Spill Point is rather arbitrary this time. It is the last point that may be included in the reservoir: if the next one (sorted by increasing depth) was included, the thickness of the reservoir would overpass the maximum admissible value.

The "Forbidden types" of control points

Up to now, all the control points have directly been used in order to derive the Spill characteristics. There exists a second type of control point: the forbidden type ones. This information is not used for the calculation of the Spill characteristics. They are simply double-checked a posteriori.

A forbidden outside point is a location which must result as either inside or unknown. Conversely, a forbidden inside point is a location which must result as either outside or below or unknown.

If in a map (usually a simulation outcome), one of these constraints is not fulfilled, the whole map is considered as not acceptable and is discarded from the final statistics.

Limits of the algorithm

It is essential to understand the behavior of the algorithm in the following simplified scenarios.

Let us consider the case of a synclinal where the top of the structure is constrained to belong to the reservoir whereas a point located on its flank is supposed to be outside. The Spill (considered as being the deepest horizontal plane where both constraints are fulfilled) is obviously located at the elevation of the outside control point.
Let us now consider the opposite case where the outside control point is at the top of the structure and the inside control point is on the flank. In principle, the situation should be symmetric with the same result for the elevation of the Spill. But if we consider the volume of the reservoir now: the volume of the reservoir controlled by the inside control point and located above the spill has its volume reduced to zero. That is the reason why such a map is considered as not acceptable.

Converting Unknown volumes into Inside ones

As explained previously, the Spill point calculation may delineate volumes located above the Spill, but where the algorithm cannot decide if it belongs to the reservoir or not: these volumes are called unknown.

Then, if these volumes are discarded from the global statistics, the results are biased: the unknown volumes are always considered as outside. Another possibility is to convert them all empirically to inside in order to get another biased estimate (by excess this time).

In addition to the bias, this latter operation can lead to contradictions if the maximum reservoir thickness criterion has been taken into account, as explained in the next figure:

The volume A is considered outside and B inside the reservoir. The volumes C and D are initially unknown. If we convert them into inside, the maximum reservoir thickness constraint will not be fulfilled any more for the volume C. We could imagine to move the spill upwards until the constraint is satisfied, but then we should also move the Spill Point in a new location. Instead, we have considered that such a map should rather be considered as not acceptable.