KNA - Discretization Point Optimization

To access this dialog:

Using the Advanced Estimation dialog, select Optimize from the left-hand menu system and then select the Optimize Discretisation sub-panel.

This panel is used to determine the optimum number of discretisation points for calculating the Block covariance (BLKCOV). A 3D array of discretization points is used to represent the model cell for the purpose of calculating the block and block-point covariances that are required for setting up the kriging equations.

This panel is only visible if Supervisor data is not being imported. You decide this using the Scenario Setup screen.

The points are located symmetrically within the model cell so that each point represents an equal 3D rectangular volume. Further details of the Block covariance are given at the end of this page.

In general terms as the number of points increases the accuracy of the covariance increases but the processing time also increases. In the example graphic the block covariance decreases from about 3.667 when there is 1 discretization point in X to 3.637 when there are 8 points. However, there is no real gain in accuracy after about 6 points.

Note: Advanced Estimation is part of the Studio RM toolset. Additional licensing modules aren't required.

Field Details:

You use this panel to define the number of discretisation points within a model cell in each of the X, Y and Z directions. This is done by entering the minimum, number of intervals and increment for each of the three directions as described in the Optimize section.

The block covariance calculation also needs the block dimensions which are shown in the Base block size area. The initial dimensions are set in the Select Locations panel either from the parent cell values if a prototype model has been defined or from the Initial block size values entered manually. The dimensions can also be reset by editing the Base values in the Optimize Block Sizes sub-panel. You should always check that the dimensions shown in the Base block size area are your required values.

Example - Discretization

Inputs- Variogram Model

The variogram model has been selected by clicking the required model in the Variogram Model area of the Optimize panel. This example is based on a single structure spherical anisotropic model with the following parameters:

Nugget: 0.35 Sill: 3.87 Rotation: 22.5o around Z
Ranges: X – 82.9, Y – 93.2, Z – 25.6

Inputs – Block Size

The block dimensions are defined by their Base values shown in the Base block size area.

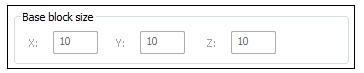
The current Base block size is displayed here for reference purposes. The values can be changed by editing the Base values on the Optimize Block Sizes sub-panel.

Inputs – Discretization Points

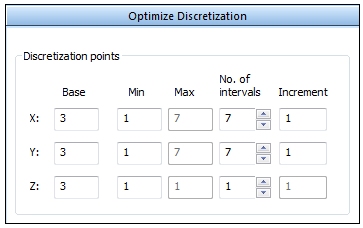
The number of points in X and Y range from 1 to 7 while the number in Z is fixed at 3.

Increment values will be rounded up to the nearest integer

Inputs – Combinations

The Test all combinations option is selected.

This makes a total of 10x10x1 = 100 KNA runs. Click Run Tests to start the KNA runs. A progress message is displayed in the Command Window.

Outputs

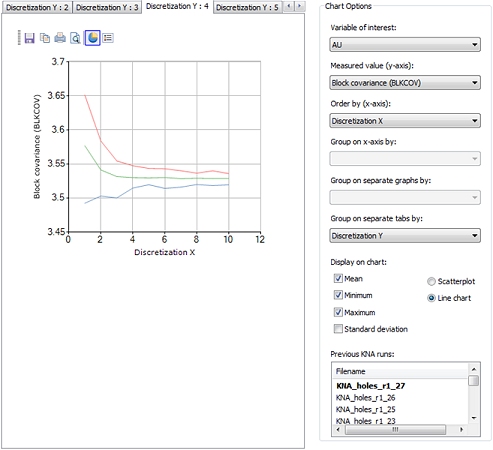
The chart below shows the number of discretization points in X, on the X axis, and the Block covariance on the Y axis.

Discretization Y has been chosen from the Group on separate tabs by selection box. This means there is a separate tab for each of the 10 values of Discretization Y. The tab for 6 discretization points in Y is displayed.

The colored lines show the mean (green), minimum (blue) and maximum (red) values of the Block Covariance.

It can be seen that there is no real change in the mean Block covariance value after 4 discretization points in both X and Y, with 3 in Z, so there is no point in selecting more than that.

The full set of results are available in the KNA results file KNA_holes_r1_27 which can be opened in the Table Editor from the Project Files control bar.

Block Covariance Value

The Block Covariance (BLKCOV) value is calculated as the difference between the total sill of the variogram model and the average value of the variogram over the entire block. The average variogram value is approximated as the average value between each pair of discretization points. This is acceptable when pairing a discretization point with a different discretization point but when a discretization point is paired with itself the variogram value will equal the nugget which will under-estimate the average value in the 3D rectangular volume that the point represents.

To compensate for the under-estimation an additional discretization point is generated which lies at random within each 3D rectangular volume that each discretization point represents. The variogram value for the point with itself is then calculated as the value between the central discretization point and the random point. This value is used instead of the nugget variance when calculating the average value of the variogram over all pairs of points.

The random component means that multiple runs with the same set of parameters will not give exactly the same results. However a review of the mean, minimum and maximum values is more than sufficient to determine a suitable number of discretization points.

	Related Topics
	Select Locations Optimize Optimize Block Sizes Optimize Search Parameters