Cross Variogram Coregionalization

When modelling Cross Variograms, the model needs to be positive semi-definite for the bivariate case. This condition is a requirement for the estimation process.

To ensure the condition is met, you need to first select the appropriate directional models from the Coregionalization tab of the variogram's Continuity Models component (its parent component). After selection, the univariate variogram models display in the same window as the cross variogram. This allows you to visually inspect the results when you start modelling the cross variogram. See Insert a Cross Variogram Using Continuity Models.

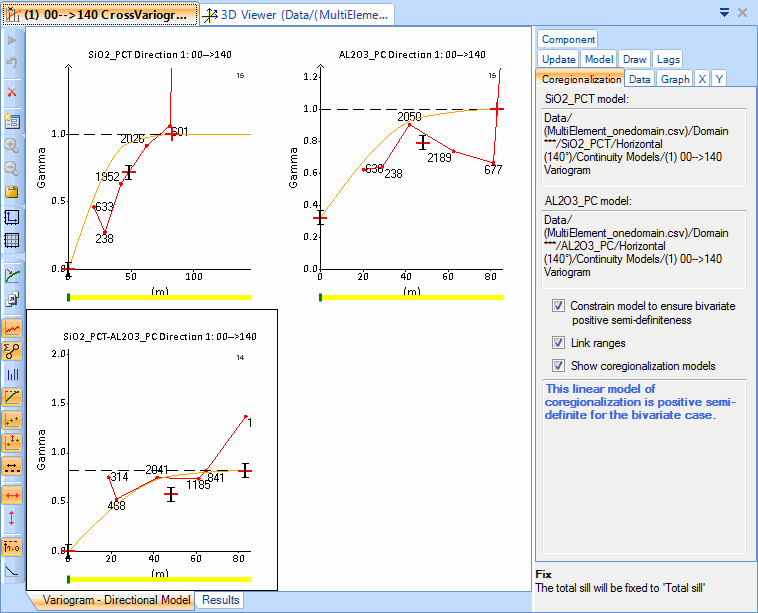
The image below shows an example of the Main Canvas after the assays for cross variogram modelling have been selected. The two univariate variograms display at the top of the window and the cross variogram at the bottom. At this point, your cross variogram model is unlikely to be positive semi-definite and the Coregionalization tab should look similar to the image below.

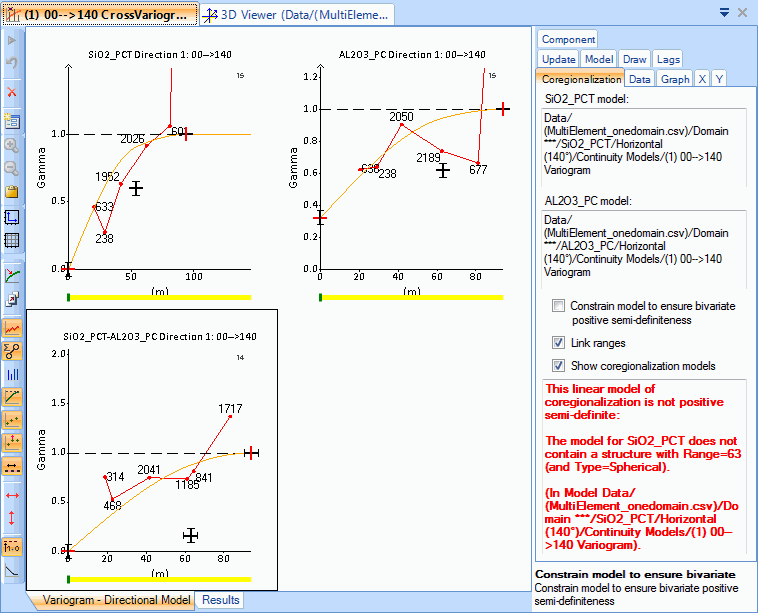
There are two reasons why a model may not be positive semi-definite.

1. The cross-variogram model must be made up only of structures that exist in both the specified univariate variogram models. For example, if both univariate models are made up of a nugget and a spherical structure, with given sills and ranges, the cross-variogram model may contain only a nugget and spherical structure with the same range. If this condition is not met, it is reported on the Coregionalization tab as shown above.
2. The ranges for each corresponding structure must be the same. This is easiest when Link ranges is enabled in the Coregionalization tab. By moving the structures in the cross-variogram, the ranges of the corresponding structures of the univariate variogram models move accordingly.

   Note: Moving the ranges in the univariate models does not affect the cross variogram.

To correct the model, you can try two things.

1. Move the sills of the cross variogram or univariate models. If moving the sills of the univariate models when the ranges are not locked you may have to re-synch the ranges as discussed above.
2. Check Constrain model to ensure bivariate positive semi-definiteness in the Coregionalization tab, which sets the sills of the cross variogram structures to values that satisfy the positive semi-definiteness condition. However, it is possible that given other restrictions, such as the cross variogram model's sill to be fixed at 1, that there is no such solution, in which case you must either relax the restricting condition or move the sills of the univariate models.

   Note: You can still manually refine your model with Constrain model to ensure bivariate positive semi-definiteness enabled by moving the cross variogram structures around, but only within the bounds of a valid solution.

Once all three models have the same structures and the ranges are in order Supervisor calculates the sill determinant for each structure. If all sill determinants are greater than or equal to zero, the dialog box reports that the positive semi-definite condition has been met.

The image below shows a cross variogram that satisfies the positive semi-definiteness condition.