Output

  • Simulation Parameters:

    • Enter the Number of Realizations (of the same variable) you wish to perform simultaneously. There is no theoretical limit on this number (except the performance of the machine you are working on).
    • Each simulation is considered as a separate item stored in a single Macro Variable. Each item is attributed a rank or index (within the macro variable). The ranks are automatically generated starting from the Starting Realization and incremented by 1. If the output Macro Variable already exists (and refers to the same grid dimensions), and if an item with a given index already exists, it is replaced by the new simulation. In the Starting Realization box, enter a value for the first index to be calculated.

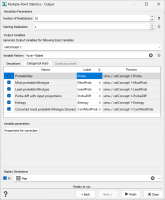
  • Output Variables: The count of items in the output list depends on the Generate Output Variables for following Input Variables selected. By default, we will store the results associated to each data variable specified on input. Click on the to edit the variables list and deselect the variables whose simulation results you do not want to store.

    The objective of the Variable Pattern parameter is to help the definition of output result names. You can edit this pattern to modify it and define the name of your choice. Click on to retrieve the default pattern: %var-%label

    The Label section is editable by a double-click for modification. The Preview enables you to see the final name associated to each output result.

    You may then specify several output variables:

    • the Simulationmacro variable where the simulations will be stored.

      If a categorical variable is simulated, the following variables will only be available. They will appear in the Categorical stats tab.

    • the Probabilitiesmacro variable with an index for each lithotype defined earlier (each category of your lithotype variable): for each node of the grid and for each lithotype, the program computes the number of simulations belonging to this lithotype. When normalizing this value to the total number of simulations, this gives a probability (between 0 and 100 with a % unit) to be in the defined lithotype.
    • the Most probable lithotypecategorical variable will store the most represented category/lithotype of the simulations (i.e. the category/lithotype with the highest proportion).
    • the Least probable lithotypecategorical variable will store the least represented category of the simulations (i.e. the category with the smallest proportion).
    • the Proba diff with input proportionsmacro variable with an index for each category defined earlier (each category of your lithotype variable): absolute value of the difference between the input proportions (global or local) and proportions/probabilities calculated from the simulations.

    • the Entropynumerical variable will represent the average level of uncertainty inherent to the variable’s possible outcomes. It is calculated by the following formula:

      where pi is the probability (between 0 and 1) of the lithotype i and log represents the logarithm base 2.

    • the Corrected most probable lithotype (Soares): The Soares correction is meant to correct the lithotype probabilities after the simulation by taking into account the global probabilities. Using this algorithm, a new most probable lithotype can be deduced. This algorithm is detailed in:

      • Soares (1992): Geostatistical Estimation of Multi-PhaseStructures, Mathematical Geology, Vol. 24, No.2, 149-160.
      • Soares (1998): Sequential Indicator Simulation with Correction for Local Probabilities, Mathematical Geology, Vol. 30, No.6, 761-765.

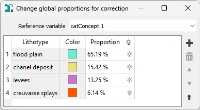
      If the Corrected most probable facies (Soares) variable is asked to be stored, click the Proportions for correction button to modify the proportion of each input lithotype. By default, the proportions will be the same as the ones defined on input.

      Note: When one or more realizations of the macro variable are not defined on a node, this node will not be taken into account in the calculations. Proportions are calculated on the same number of nodes for all the realizations.

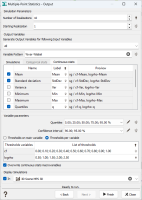
    If a numerical variable is simulated, the following variables will only be available. They will appear in the Continuous stats tab.

    • Mean: gives the mean value of the set of simulations on each cell or block of the grid.

    • Standard Deviation / Variance: gives the standard deviation / variance of the set of simulations on each cell or block of the grid.

    • Minimum: gives the minimal envelope of the set of simulations on each cell or block of the grid (that means that, for each node of the grid, the program selects the simulation which is the smallest one. It could be different from one node to another).

    • Maximum: gives the maximal envelope of the set of simulations on each cell or block of the grid (that means that, for each node of the grid, the program selects the simulation which is the biggest one. It could be different from one node to another).

    • Quantiles: enables the calculation of different quantiles for each cell or block of the grid. For a given quantile p, the quantile map displays the value for which there is p% of chance (i.e. p% of the simulations) that the real value z is smaller than this value. In this application, a quantile is always one of the simulation values of the macro variable.

      Click Edit to pop up the Value Definition window and customize the list of quantiles.

    • Confidence interval width: the confidence interval map represents the width of the interval which contains the real value at a given confidence level. For each node of the grid, simulated values are sorted in increasing order to compute quantiles (a quantile is always one of the simulation values of the macro variable). The p% confidence interval is based on the computation of two symmetric quantiles:

      Click Edit to pop up the Value Definition window and customize the list of confidence intervals.

    • Mean grade: for each node of the grid, the program computes the average value of the simulated values greater than or equal to the defined threshold or within the two defined thresholds.

    • Probability: for each node of the grid, the program computes the number of simulations whose the value is greater than or equal to the defined threshold or within the two defined thresholds. When normalizing this value to the total number of simulations, this gives a probability (between 0 and 1) for the node to exceed the defined threshold.

    • Accumulation: for each node of the grid, the program calculates the sum of the simulated values which are greater than or equal to the defined threshold or within the two defined thresholds, multiplied by the area or the volume of the cell. This sum is then divided by the total number of simulations.

      In 3D, a Density factor is also applied to compute masses. The density can be a constant value or defined by a variable. In this last case, the selected variable should be associated with a Mass density unit class.

      In 2D, a Thickness factor is also required. The thickness can be a constant value or defined by a variable. In this last case, the selected variable should be associated with a Length unit class.

      Depending on the type of the variable, the result can be homogeneous to a tonnage for a grade, or a volume for a thickness in 2D for example.

  • As the some results are saved in macro variables, these ones can be overwritten if they already exist by checking the Overwrite macro option. Otherwise, results will be appended (i.e. new indices will be added in the existing macro variable).
  • Select the Display Simulations toggle to display the result of the first simulation in a defined scene (2D or 3D depending on the data dimension) at the end of the run.